아래에서 설명할 부분은 머신러닝 시 멤버십 테스트 등을 할 때 사용될 것이기 때문에 가볍게 읽고 이해만 하시면 될 것 같습니다. 쉽게 설명 부분만 보셔도 됩니다.
1. 집합의 포함(Inclusion)과 배제(Exclusion) : 삼지창 모양
(1) 쉽게 설명
- A안에 1이 포함되어 있습니다. 포함은 ∈ 기호를 사용합니다.
- A안에 4는 포함되어 있지 않습니다. 포함되지 않을 때는 ∉ 기호를 사용합니다.

(2) 학술적으로 설명
원소 a가 집합 A에 포함됨 (a ∈ A), ∈기호는 왼쪽이 오른쪽의 원소이다라는 의미입니다.
- 예제 A = {1, 2, 3}일 때, 원소 1은 A에 포함되어 있다. 즉 1 ∈ A
원소 b가 집합 A에 포함되지 않을 때 = (b ∉ A)
- 예제 A = {1, 2, 3}일때, 원소 5는 A에 포함되어 있다. 즉 5 ∉ A
2. 공집합(Empty Sets) : 두 집합이 같은 원소를 갖고 있다면 두 집합은 같다.
(1) 쉽게 설명 : A집합과 B집합의 원소가 동일한 경우입니다.
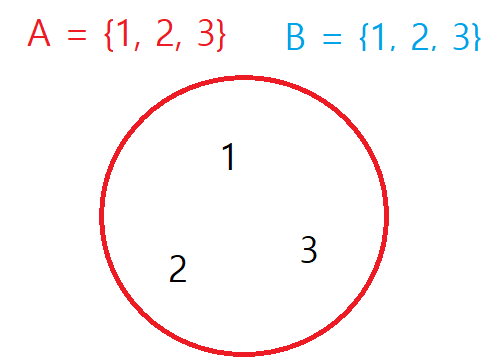
(2) 학술적으로 설명
A = B ⇔ {(∀a ∈ A) ∈ B} ∧ {(∀b ∈ B) ∈ A}를 아래와 같이 해석합니다.
- A와 B는 같다
- ∀(모든) 원소 a는 집합 A에 ∈(포함) 되고(∧), ∀(모든) 원소 b는 집합 B에 ∈(포함)된다.
3. 부분집합(Subset)과 확대 집합(Superset)
(1) 쉽게 설명
- 집합 A가 집합 B에 포함되어 있으면 A는 B의 부분집합입니다.
- 집합 B가 집합 A를 포함하고 있으면 B는 A의 확대 집합입니다.
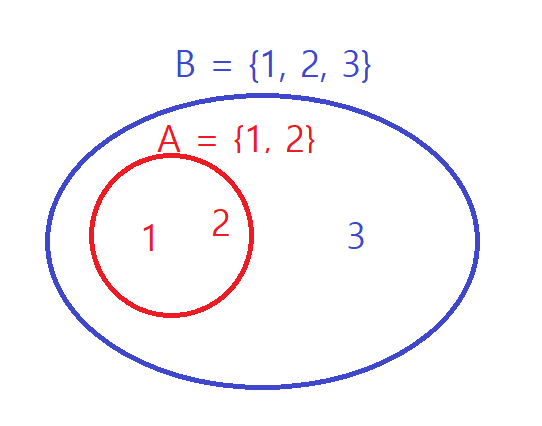
(2) 학술적 설명
- 부분집합(Subset) : 집합 A의 모든 원소가 집합 B에 포함될 때입니다.
* A⊆B ⇔ {(∀a ∈ A) ∈ B} : 집합 A의 모든 값은 집합 B에 포함된 것입니다.
* A⊆B ⇔ |A|≤|B| : 앞선 강의의 카디널 리티(원소의 개수)를 의미하며 A 원소 개수는 B의 원소의 개수보다 반드시 작거나 같아야 합니다. 당연하겠죠. 포함되어 있으니까요.
- 전체집합(Superset) : 집합 B의 관점에서 보면 됩니다. 즉, 집합 B가 집합 A를 포함하고 있으면 B는 A의 확대 집합입니다.
4. 진부분 집합(Proper Subsets)과 진확대집합(Proper Superset)
(1) 쉽게 설명
- 진부분집합 : 부분집합과 동일하나, 적어도 B의 원소 중 하나는 A에 포함되지 않아야 한다 아니다. 그림을 보시죠.
- 집합 A와 B는 동일하나, B가 3을 하나 더 가지고 있죠? 이때 A를 B의 진부분 집합이라고 합니다. 어라... 위의 확대 집합과 똑같죠? 영어도 그렇듯 비슷한 모양을 이렇게도 부르고 저렇게도 부른답니다.. 이걸 반대로 생각하면 진 확대 집합입니다.

(2) 학술적 설명
- 집합 A, B에 대해 A가 B의 subset이지만 완전히 같지는 않을 때, A는 B의 proper subset이라 한다.
- A⊂B ⇔ {(∀a ∈ A) ∈ B} ∧ [A ≠ B] : A의 원소가 모두 B에 포함되지만 A와 B는 다른 경우입니다. 이걸 반대로 생각하면 진 확대 집합입니다.
쉽게 설명 부분만 읽으셔도 프로그래밍 시 큰 어려움이 없습니다. 감사합니다.
5. 부록 : 집합 관련 수학 기호

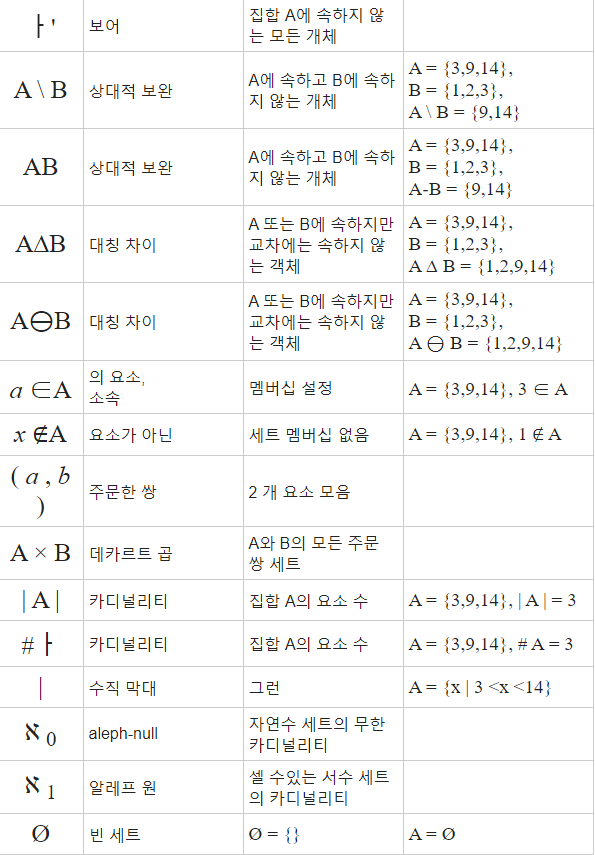

'머신러닝(Machine Learning) > 기초수학' 카테고리의 다른 글
| 기초대수학 : 단사함수, 전사함수, 전단사함수, 합성함수, 역함수 (4) | 2022.08.16 |
|---|---|
| 집합 마지막 : 집합의 분할(Partition) 개념과 수학적 증명 (5) | 2022.08.11 |
| 집합의 연산 : 단항연산(멱집합, 여집합), 다항연산(교집합, 합집합, 차집합, 대칭차집합, 데카르트곱) (2) | 2022.08.10 |
| 집합 표현 : 원소나열법, 조건제시법, 벤다이어그램 (7) | 2022.08.09 |
| 기초대수학 : 교환법칙, 결합법칙, 분배법칙, 항등원, 역원 (6) | 2022.08.07 |



