머신러닝은 수학으로부터 파생되었기 때문에 수학적 지식이 없으면 이해가 매우 어렵습니다. 그나마 다행인 점은 고등학교 2학년 정도의 눈높이라 완전 전문가의 영역이 아니므로 여러분들도 충분히 코딩할 수 있습니다.
최대한 심플하게 중요한 부분만 설명하고 넘어가겠습니다.
1. 교환 법칙(commutative property)

A와 B값이 아무리 바뀌어도 값은 동일하다입니다. 수학적으로는 아래와 같습니다.
- A☆B = B☆A
- 교환 법칙은 A와 B의 연산이 B와 A의 연산으로 바뀌어도 값이 같은 것을 의미합니다. 즉, 교환되어도 같다는 의미이지요.
- 교환 법칙 성립의 예 : 더하기, 곱, 벡터 내적 등
* 10 + 1 = 11, 1 + 10 = 11, 즉 10 + 1 = 1 + 10과 동일하죠? 따라서 교환 법칙이 성립합니다.
- 교환 법칙 성립하지 않는 예 : 빼기, 나누기, 벡터 곱하기 등
* 10 - 1 = 9, 1 - 10 = -9, 즉 10 -1 ≠ 1 -10이 됩니다. 교환 법칙이 성립하지 않습니다.
- 교환 법칙이 성립하는 경우를 아래와 같이 정리해 두었는데, 간단히 덧셈과 곱셈, 행렬의 내적 정도만 교환 법칙이 성립한다는 것을 알고 계시면 머신러닝을 수행하는데 전혀 문제가 없습니다.
2. 결합 법칙(associative property)
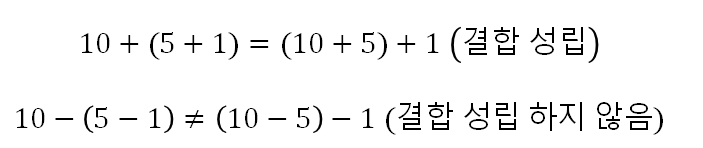
한 식에서 3개의 변수가 있고 동일한 연산이 2번일 경우 연산의 순서가 어떻게 바뀌더라도 결괏값은 동일한 것을 뜻합니다. 어려우니 예를 들어 설명하겠습니다.
- (A☆B)☆C = A☆(B☆C)
- 결합 법칙 성립의 예 : 더하기, 곱, 벡터 내적 등
* (10 + 1) + 4 = 10 + (1 + 4) 같은 경우 두 항 모두 15를 가집니다. 또한 3개의 변수와 동일한 2번의 연산이 사용되었죠?
- 결합 법칙이 성립하지 않는 예 : 빼기, 나누기, 벡터 곱하기 등
* (10 - 1) - 4 ≠ 10 - (1 - 4) 같은 경우 왼쪽 항은 5, 오른쪽 항은 13이 되어 다르다는 것을 알 수 있습니다.
3. 분배 법칙(Distributive Property)
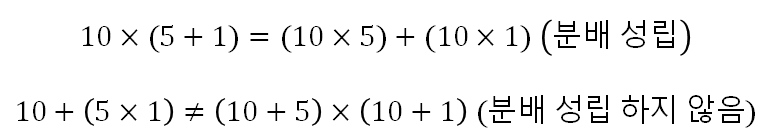
한식에 3개 이상의 변수가 있으며 다른 연산이 2번일 경우 연산이 분배되더라도 값이 동일한 경우입니다.
- A☆(B●C) = A☆B●A☆C, 좌 분배 법칙(Left hand)
- (B●C)☆A = B☆A●C☆A, 우 분배 법칙 (right hand)
- 분배 법칙 성립의 예제 : ☆가 곱하기로 구성
* 10 × (2 + 3) = 10 × 2 + 10 × 3 = 50
- 분배 법칙 성립하지 않는 예제 :☆가 더하기/나누기/빼기 등으로 구성
* 10 + (2 × 4) ≠ (10 + 2) × (10 + 4) : 좌현의 경우 18, 우현의 경우 168 완전히 다르죠?
4. 항등원(identities)
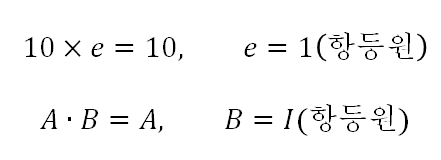
함수에 어떤 값을 넣어도 나 자신이 나오는 함수입니다. 조금 어렵게 말하면 어떤 값 x에 연산 f를 하였을 경우, 결과 값이 원래의 값인 x가 나오게 되는 것이고 f(x) = x와 같습니다. 이와 반대되는 의미는 상수 함수인데 f(x)=c와 같이 다른 값이 나오는 것입니다.
- 예제 : a ☆ e = a, 여기서 e가 항등원입니다.
* a + e = a ==> e = 0, 덧셈에 대한 항등원은 0이 됩니다.
10 + e = 10 ==> e = 0
* a × e = a ==> e = 1, 곱셈에 대한 항등원은 1이 됩니다.
10 × e = 10 ==> e = 1
5. 역원(Inverse)
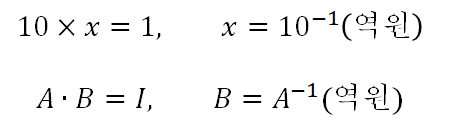
항등원이 나오게 하는 값을 역원이라고 합니다. 이는 아래 예제를 통해 알아보겠습니다.
- 예제
* a + x = e = 0 ==> a + x = 0 ==> x = -a
10 + x = 0 ==> x = -10
* a × x = e = 1 ==> a × x = 1 ==> x = a^-1
10 × x = 1 ==> x = 10^-1 or 1/10
머신러닝을 위한 첫걸음 선형대수학의 기본을 알아보았습니다. 개념 위주로 가볍게 생각하시기 바랍니다. 감사합니다.
'머신러닝(Machine Learning) > 기초수학' 카테고리의 다른 글
| 기초대수학 : 단사함수, 전사함수, 전단사함수, 합성함수, 역함수 (4) | 2022.08.16 |
|---|---|
| 집합 마지막 : 집합의 분할(Partition) 개념과 수학적 증명 (4) | 2022.08.11 |
| 집합의 연산 : 단항연산(멱집합, 여집합), 다항연산(교집합, 합집합, 차집합, 대칭차집합, 데카르트곱) (2) | 2022.08.10 |
| 집합의 포함 관계 : 포함과 배제, 공집합, (진)부분집합과 (진)확대집합, 집합관련 수학기호 (11) | 2022.08.09 |
| 집합 표현 : 원소나열법, 조건제시법, 벤다이어그램 (7) | 2022.08.09 |



