기초대수학 : 단사함수, 전사함수, 전단사함수, 합성함수, 역함수

 함수가 어떻게 주식에서 사용되는지 그리고 머신러닝에 어떤 식으로 적용되는지 설명드리겠습니다. 그리고 각 함수들의 역할과 기능에 대해서 간략히 말씀드리고 그림을 통한 예제를 많이 넣었으니 참고하세요.

 

 함수란 어떤 입력 A를 넣었을 때 출력 B가 나오게하는 기계라고 생각하시면 됩니다. 빵 만드는 기계에 부산 밀가루를 넣으면 딸기 빵이 되고 경주 밀가루를 넣으면 크림빵이 된다고 했을 때 아래 그림과 같이 표현합니다.

반응형

 

함수의 표현

 위의 그림을 조금더 수학적으로 표현하면 아래 그림과 같습니다. 아래 그림처럼 빵 만드는 기계 함수 f에 입력(Domain) A를 넣으면 출력(Codomaion) B가 나오는 것입니다.

함수의 표현

 

 여기까지 이해하셨다면, 함수의 기본을 모두 이해하신것과 동일합니다. 이때 함수의 조건을 잠깐 알아보겠습니다.

 

 (1) 하나의 입력은 적어도 하나의 출력에 대응해야 합니다. 아래 그림을 보시면 A2가 혼자 놀고 있죠? 이렇게 되면 함수가 아닙니다.

함수가 안되는 경우1

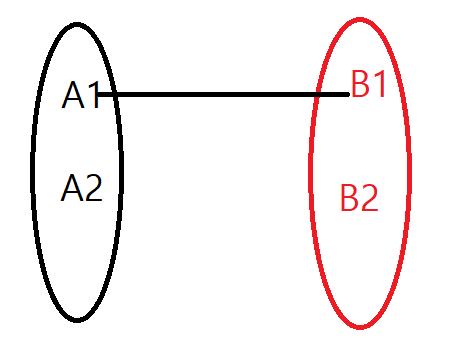
  (2) 하나의 입력은 두개의 출력에 대응이 되면 안 됩니다. 아래 그림을 보시면 A2가 B1과 B2 모두와 대응되고 있죠? 이렇게 되면 함수가 아닙니다.

함수가 안되는 경우2

 

 이제 입력이 출력과 어떻게 대응되느냐에 따라 단사함수, 전사 함수, 전단사 함수, 합성함수, 역함수라고 표현하는데 간단하니 개념만 잡고 넘어가겠습니다.

 

1. 단사함수(injective) 

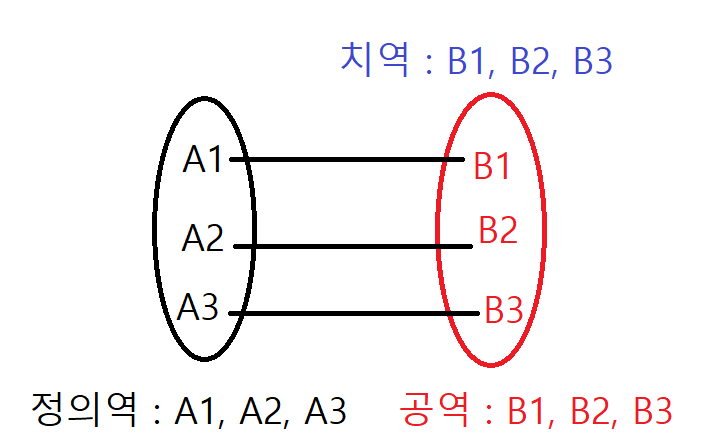
 정의역(Domain)의 원소가 공역(CoDomain)의 원소 수와 같거나 적은 경우. 즉 치역(Range)이 공역과 일치하지 않는 경우입니다. 그림과 같이 B3가 혼자 놀고 있는 경우입니다.

단사함수( injective )

2. 전사함수(sujective) 

 단사 함수와는 반대 현상으로 아래 그림과 같이 공역과 치역이 동일하고 하나의 공역이 다수의 정의역을 포함하는 것입니다. 그림에서 B1이 A1과 A2를 포함하고 있으므로 전사 함수입니다.

전 사함수 ( sujective )

3. 전단사 함수(bijective)

 전사 함수와 단사 함수를 모두 만족하는 것으로 모든 값들이 일대일 대응이라 생각하시면 될 것 같습니다.

전단사함수 ( bijective )

4. 합성함수(Composite)

 A에서 B로 다시 B에서 C로.... 계속 함수가 연결되는 것입니다. 이 부분이 머신러닝의 모든 것, 또는 끝이라 할 수 있습니다. 모든 머신러닝은 레이어로 구성되어 있기 때문에 합성함수 그 자체라고 보시면 됩니다.

 주식으로 설명드리면 삼성전자의 A1(매출액), A2(수급), A3(차트)가 만족할 때 B1(200만 원), B2(매수), B3(오후 1시)를 수

합성함수(Composite)

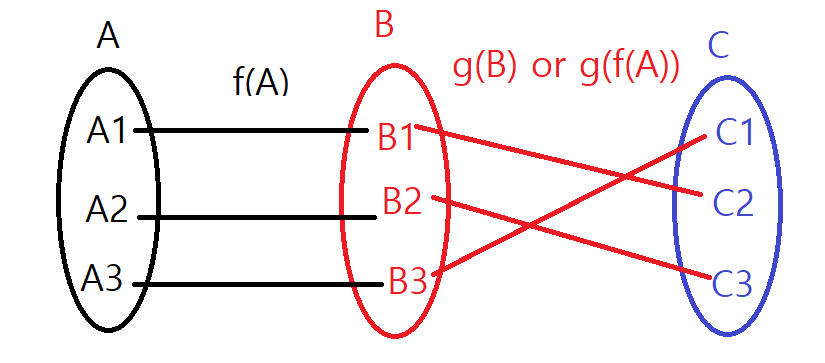
행하고 C1(10주), C2(2번 분할), C3(추격매수)를 수행하게끔 되는 것이 바로 머신러닝입니다. 이런 식으로 계속 학습을 시켜 최적의 A, B, C값을 찾아 승리하는 공식을 찾는 것이 머신러닝입니다.

 수식으로 나타내면 최종 출력 = g(f(A))로 나타낼 수 있습니다.

 

5. 역함수(Inverse)

 역함수는 f에 B를 넣을 때 다시 A가 나오게 되는 함수를 뜻합니다. 즉 반대되는 개념이라 생각하시면 됩니다. 그리고 역함수도 앞서 말씀드린 함수와 동일하게 2가지 조건을 만족해야 합니다.

 (1) 하나의 입력은 적어도 하나의 출력에 대응해야 합니다. 즉 단사 함수의 경우 예시처럼 B3 하나가 남을 수 있으므로 역함수가 성립되지 않습니다.

단사함수( injective)와 단사함수 역함수

 

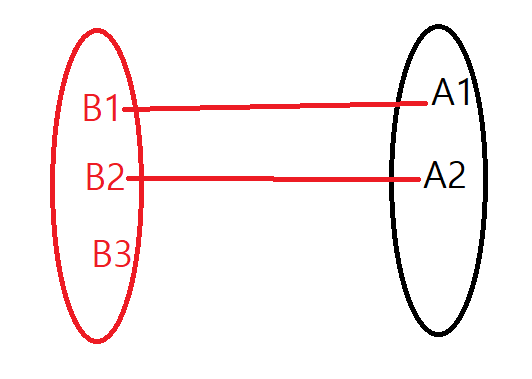
  (2) 하나의 입력은 두 개의 출력에 대응이 되면 안 됩니다. 즉 전사 함수와 같이 B1이 다수의 정의역의 선택을 받을 경우 역함수 시 B1이 다수의 공역을 선택하게 되므로 역함수가 성립되지 않습니다. 

 

전사함수 (sujective)와 전사함수 역행렬

 

 위조건에 의해 역함수가 성립되는 함수는 전단사 함수뿐입니다. 완전히 1:1 대응이 되어야 역함수가 생성될 수 있습니다. 이렇게 간단하게 함수의 성질에 대하여 알아보았습니다. 수고하셨습니다.