머신러닝에서 중요한 대수 함수 중 함수의 종류와 연산에 대하여 간단히 말씀드리겠습니다. 실제 코딩 들어갈 때 또 한 번 더 말씀드리겠으니 간단하게 이런 게 있구나라는 개념만 잡으시면 될 것 같습니다.
1. 대수함수란?
함수와 함수간 대수식(덧셈, 뺄셈, 나눗셈, 곱셈, 거듭제곱 등)으로만 표현된 함수를 말합니다. 대수 함수에 무엇이 있는지 아래에서 알아보겠습니다.
2. 대수 함수의 종류
(1) 상수 함수(Constant Function) : 어떤 입력을 넣더라도 무조건 1개 출력이 나옵니다(변화가 없다라고도 표현).
- 함수적 표현 : 정의역 x에 어떤 값을 넣더라도 상수 y가 나오는 것이고 아래 수식과 동일합니다.
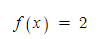
- 위 수식을 보면 x에 어떤 값을 넣더라도 2가 나오게 됩니다.
- 그래프적 표현하면 아래 그림과 같으며, 정의역의 모든 원소는 1개의 치역을 가지게 되는 것이죠.
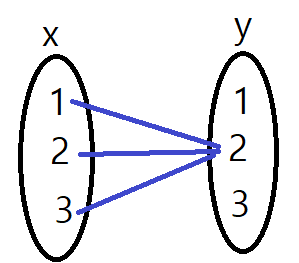
- 이를 공간 좌표에 나타내면 아래와 같습니다. x에 어떤 값이 들어가도 2가 출력되는 것을 확인할 수 있죠. 이것이 상수 함수입니다.
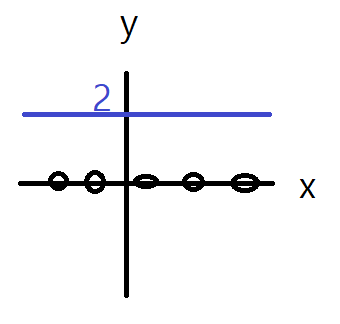
(2) 일차함수(Linear Function)
함수적 표현 : 수식으로는 아래와 같으며, a는 x의 기울기이며, b는 y축의 절편을 뜻합니다.
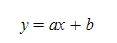
쉽게 설명드리기 위해 아래와 같은 예제로 알아보도록 하겠습니다.
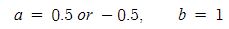
a와 b의 값이 위와 같을 때 그래프는 아래와 같습니다.
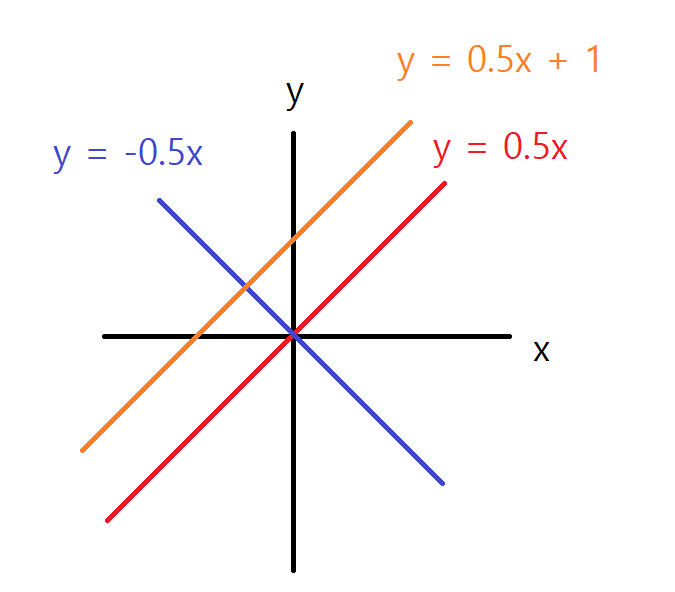
a는 +일 때와 -일 때에 따라 기울기 방향이 바뀌게 되고, a의 크기가 ∞(무한대)에 가까워질수록 기울기는 급해지며, a의 크기가 0에 가까워 질 수록 기울기는 완만해집니다. b는 y절편으로 그래프가 b만큼 y축에서 이동한 것을 확인할 수 있습니다.
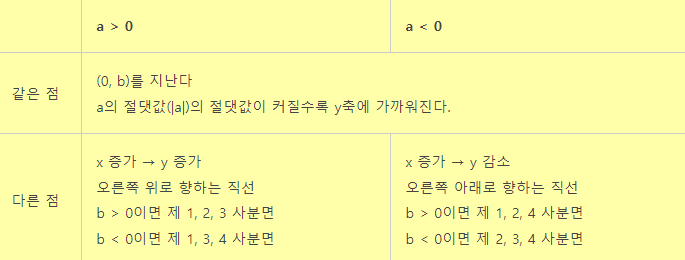
이러한 특성을 정리하면 아래 표와 같습니다(그냥 눈으로 쓱~ 보고 가시면 됩니다).
(3) 멱함수(Power function) : 거듭제곱의 지수를 고정하고 밑을 변수로 하는 함수이며, 아래 수식과 같이 나타냅니다.
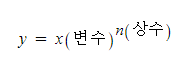
위 수식을 그림으로 한번 나타내 보겠습니다.
- 상수가 짝수인 경우 : 음이 될 수 없으므로 아래 그림과 같고 상수가 커질 수 록 기울기가 커집니다.
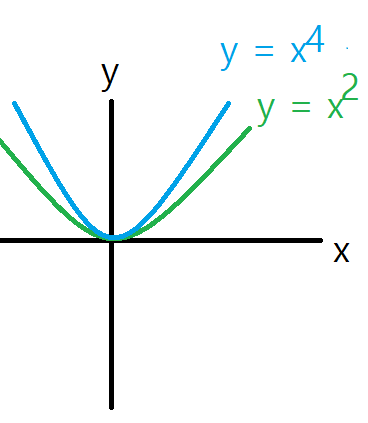
- 상수가 홀수인 경우 : 아래 그림과 같고 상수가 커질 수 록 기울기가 커집니다.
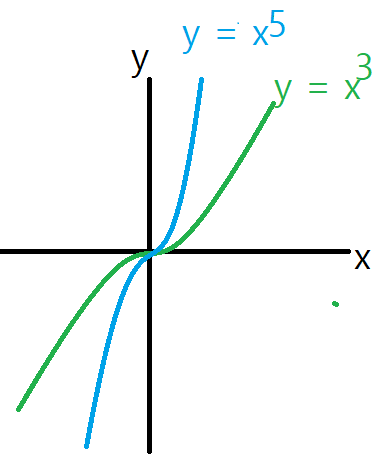
(4) 유리함수 : x값이 ∞로 갈수록 0에 가까워지며 점근선이라고도 부릅니다. 이때 y축 값도 무한이 커지며, 발산하게 됩니다.
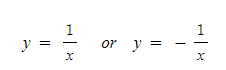
그림으로 나타내면 아래와 같습니다. x축과 y축으로 무한이 가까워지며, 점근선이라 표현합니다.
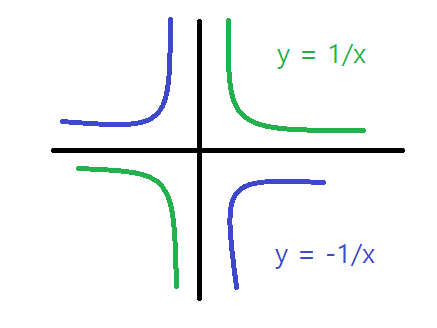
(5) 무리함수 : x축 값에 따라, y축 값이 증가하다가 어느 순간부터 증가량이 한계가 생기는 특징이 있습니다.
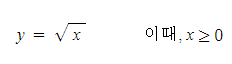
그림으로 나타내면 아래와 같습니다.
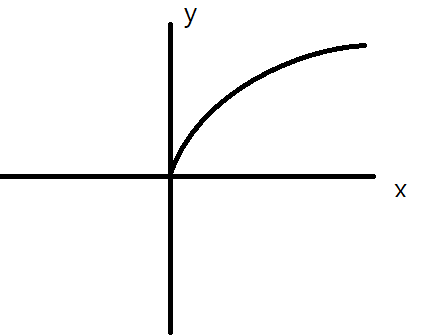
3. 함수의 연산
(1) 상수곱(Constant Multiple) : f(x)를 a배 한 것과 동일하다.
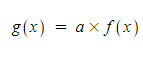
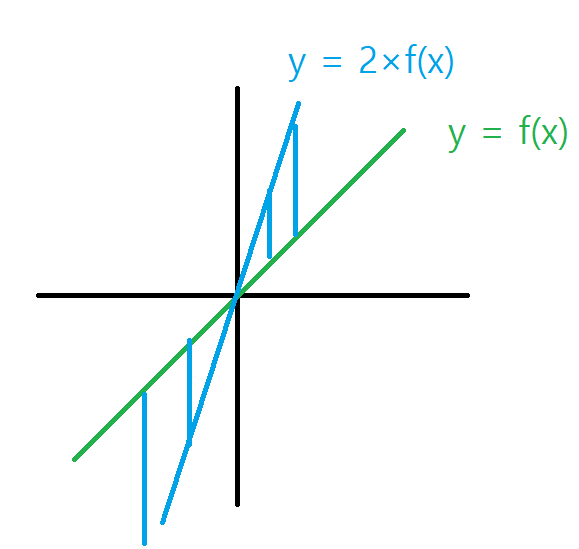
- 위 그림을 보시면, 상수곱은 함수의 기울기를 변화시킵니다.
(2) 더하기(Addition) : f(x)와 g(x)를 더하는 것으로 신호처리 등에 상당히 많이 쓰입니다.
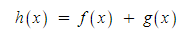
그림으로 나타내면 아래와 같으며, x축 값에 대응하는 모든 y값을 더한다고 생각하시면 됩니다.
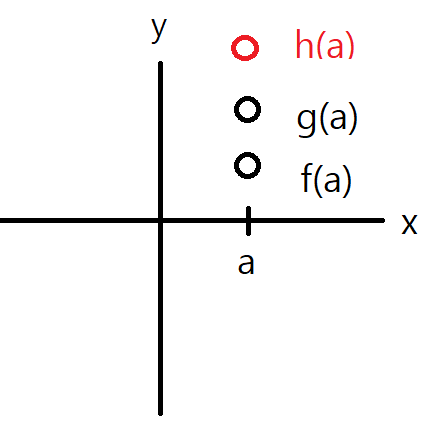
(3) 이차함수의 합(Quadratic function) : 2차 함수와 1차 함수의 합으로 구성된다고 생각하시면 됩니다.
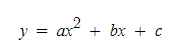
(4) 삼차 함수의 합(Cubic Function) : 3차/2차/1차 함수의 합입니다.
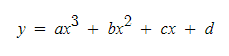
(5) 다항식 함수의 합(Polynominal Function) : n차 다항함수의 합입니다.
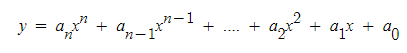
이상 포스팅을 마치겠습니다. 혹시 질문 사항 있으면 언제든 댓글 달아 주시고 함수의 합은 머신러닝과 신호처리의 꽃과 같습니다. 감사합니다
'머신러닝(Machine Learning) > 기초수학' 카테고리의 다른 글
| 함수의 대칭 이동과 변환(평행/수직) 그리고 정반사 및 우/기함수 (10) | 2022.09.25 |
|---|---|
| 초월함수 : 지수함수, 로그함수, 삼각함수, 쌍곡선함수 (6) | 2022.09.22 |
| 기초대수학 : 단사함수, 전사함수, 전단사함수, 합성함수, 역함수 (4) | 2022.08.16 |
| 집합 마지막 : 집합의 분할(Partition) 개념과 수학적 증명 (4) | 2022.08.11 |
| 집합의 연산 : 단항연산(멱집합, 여집합), 다항연산(교집합, 합집합, 차집합, 대칭차집합, 데카르트곱) (2) | 2022.08.10 |



