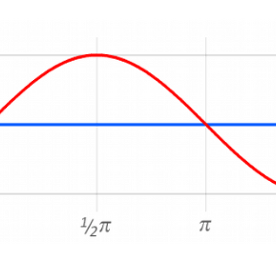
 초월함수 : 지수함수, 로그함수, 삼각함수, 쌍곡선함수
머신러닝을 위한 기초수학으로 초월함수를 알아보겠습니다. 특성이나 기타 자세한 설명은 고등수학을 보시면 될 것 같고 아 이런 것이 있구나라고 눈으로 보시고 넘어가시면 될 것 같습니다. 목차 1. 지수함수 2. 로그함수 3. 삼각함수 4. 쌍곡선함수 1. 지수함수(Exponential Functions) 지수함수는 x값에 따라 기울기가 급격히 커지는 함수라고 생각하셔도 될 것 같습니다(그림참조). 아래 지수함수 수식에서 a는 상수이며, x는 변수입니다. 즉, a에는 0, 1, 2, 3, 4등의 수가 들어갈 수 있고 x는 임의의 수라는 것입니다. 특징으로는 그림을 확인해 보면 지수함수는 x가 0일때 반드시 1이 되므로 y절편에서 1을 반드시 지나게 됩니다. 상수가 정수가 될 경우 증가하는 추세를 나타내고, 상..
더보기
초월함수 : 지수함수, 로그함수, 삼각함수, 쌍곡선함수
머신러닝을 위한 기초수학으로 초월함수를 알아보겠습니다. 특성이나 기타 자세한 설명은 고등수학을 보시면 될 것 같고 아 이런 것이 있구나라고 눈으로 보시고 넘어가시면 될 것 같습니다. 목차 1. 지수함수 2. 로그함수 3. 삼각함수 4. 쌍곡선함수 1. 지수함수(Exponential Functions) 지수함수는 x값에 따라 기울기가 급격히 커지는 함수라고 생각하셔도 될 것 같습니다(그림참조). 아래 지수함수 수식에서 a는 상수이며, x는 변수입니다. 즉, a에는 0, 1, 2, 3, 4등의 수가 들어갈 수 있고 x는 임의의 수라는 것입니다. 특징으로는 그림을 확인해 보면 지수함수는 x가 0일때 반드시 1이 되므로 y절편에서 1을 반드시 지나게 됩니다. 상수가 정수가 될 경우 증가하는 추세를 나타내고, 상..
더보기
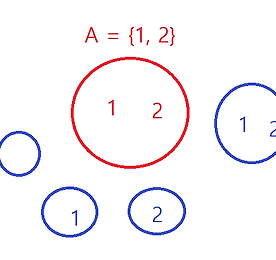 집합의 연산 : 단항연산(멱집합, 여집합), 다항연산(교집합, 합집합, 차집합, 대칭차집합, 데카르트곱)
집합의 연산(Operations on Sets)이란 일정한 규칙을 통해 새로운 집합을 만들어 내는 과정입니다. 머신러닝에서 자주 관련 식들이 등장할 예정이니 이해하고 넘어가시면 큰 도움이 될 것 같습니다. 1. 단항 연산(Unary Operations) : f : A ⇒ B 단항 연산이란 하나의 집합에서 새로운 집합을 만들어 내는 것입니다. (1) 멱집합(power of sets) : 집합 A의 모든 부분집합들을 원소로 갖는 집합. 아래 그림의 파란색이 A의 멱집합 입니다. - 예로 A = {1, 2}이면 A의 멱집합은 아래와 같습니다. - A의 멱집합 : {}, {1}, {2}, {1, 2}, 즉 A의 모든 부분집합입니다. 파란색 동그라미들과 동일합니다. - 아래는 수학적 증명입니다. - P(A) = ..
더보기
집합의 연산 : 단항연산(멱집합, 여집합), 다항연산(교집합, 합집합, 차집합, 대칭차집합, 데카르트곱)
집합의 연산(Operations on Sets)이란 일정한 규칙을 통해 새로운 집합을 만들어 내는 과정입니다. 머신러닝에서 자주 관련 식들이 등장할 예정이니 이해하고 넘어가시면 큰 도움이 될 것 같습니다. 1. 단항 연산(Unary Operations) : f : A ⇒ B 단항 연산이란 하나의 집합에서 새로운 집합을 만들어 내는 것입니다. (1) 멱집합(power of sets) : 집합 A의 모든 부분집합들을 원소로 갖는 집합. 아래 그림의 파란색이 A의 멱집합 입니다. - 예로 A = {1, 2}이면 A의 멱집합은 아래와 같습니다. - A의 멱집합 : {}, {1}, {2}, {1, 2}, 즉 A의 모든 부분집합입니다. 파란색 동그라미들과 동일합니다. - 아래는 수학적 증명입니다. - P(A) = ..
더보기
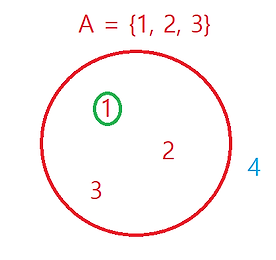 집합의 포함 관계 : 포함과 배제, 공집합, (진)부분집합과 (진)확대집합, 집합관련 수학기호
아래에서 설명할 부분은 머신러닝 시 멤버십 테스트 등을 할 때 사용될 것이기 때문에 가볍게 읽고 이해만 하시면 될 것 같습니다. 쉽게 설명 부분만 보셔도 됩니다. 1. 집합의 포함(Inclusion)과 배제(Exclusion) : 삼지창 모양 (1) 쉽게 설명 - A안에 1이 포함되어 있습니다. 포함은 ∈ 기호를 사용합니다. - A안에 4는 포함되어 있지 않습니다. 포함되지 않을 때는 ∉ 기호를 사용합니다. (2) 학술적으로 설명 원소 a가 집합 A에 포함됨 (a ∈ A), ∈기호는 왼쪽이 오른쪽의 원소이다라는 의미입니다. - 예제 A = {1, 2, 3}일 때, 원소 1은 A에 포함되어 있다. 즉 1 ∈ A 원소 b가 집합 A에 포함되지 않을 때 = (b ∉ A) - 예제 A = {1, 2, 3}일때,..
더보기
집합의 포함 관계 : 포함과 배제, 공집합, (진)부분집합과 (진)확대집합, 집합관련 수학기호
아래에서 설명할 부분은 머신러닝 시 멤버십 테스트 등을 할 때 사용될 것이기 때문에 가볍게 읽고 이해만 하시면 될 것 같습니다. 쉽게 설명 부분만 보셔도 됩니다. 1. 집합의 포함(Inclusion)과 배제(Exclusion) : 삼지창 모양 (1) 쉽게 설명 - A안에 1이 포함되어 있습니다. 포함은 ∈ 기호를 사용합니다. - A안에 4는 포함되어 있지 않습니다. 포함되지 않을 때는 ∉ 기호를 사용합니다. (2) 학술적으로 설명 원소 a가 집합 A에 포함됨 (a ∈ A), ∈기호는 왼쪽이 오른쪽의 원소이다라는 의미입니다. - 예제 A = {1, 2, 3}일 때, 원소 1은 A에 포함되어 있다. 즉 1 ∈ A 원소 b가 집합 A에 포함되지 않을 때 = (b ∉ A) - 예제 A = {1, 2, 3}일때,..
더보기
.link_tit