앞서 오차함수의 개념을 알아보았다. 이제 오차함수가 어디에 어떻게 사용되는지 심층적으로 알아보겠다. 물론 앞서 설명한 개념과 가우스 확률분포의 적분이 오차함수인 것인 이해 해야 한다.
1. 오차함수 정리 : 통신 관점
아래의 가우시안 확률분포 식을 보면 시그마(분산)에 따라서 높이와 x축이 달라지는 것을 알 수 있다. 앞서 말했지만 아래 그래프를 적분하면 오차함수라고 하였다(가우시안 확률분포의 넓이는 오차이다). 즉, 그래프가 x축에 넓게 퍼져 있으면(시그마가 3인 경우) 그만큼 에러가 날 확률이 높아지게 된다. 이를 통신관점에서 한번 바라보자.

우리가 가우시안 잡음이라고 통신에서는 많이 이야기 한다. 아래 그림의 가우시안 잡음은 모든 값을 다 더하면 0이 되는, 즉 평균이 0이 되는 잡음을 말한다.

이때, 시그마가 1인 경우는 진폭이 1인 것이고, 시그마가 3인 것은 진폭이 3인 것이다. 시그마가 3인 경우 분산이 커(진폭이 커) 시그마가 1인 경우보다 에러가 날 확률이 높아 성능이 더 좋지 않게 된다.
즉, 통신관점에서 가우시안 잡음은 진폭의 분포라고 봐도 무방하다. 그러면 우리가 원하는 신호를 1과 1 또는 E와 -E로 신호를 보낸다고 생각해 보자.

위 그림에서 E와 -E로 신호를 보낼 때 잡음등이 섞여 E의 경계점을 넘어 -E로 넘어가는 신호 또는 반대의 신호들이 생기게 된다. 즉, E와 -E가 정확히 겹치는 중간지점(detection point)을 기준으로 서로의 값이 넘어가는 순간 에러가 발생하게 되는 것이다. 그러면 상식적으로 두 값이 겹쳐지는 지점이 넓어지면 당연히 에러가 발생할 범위가 넓어지게 된다. 앞서 시그마가 3인 경우 x축의 면적이 넓어져 두 값이 더 많이 겹쳐지게 되므로 시그마가 1인 경우보다 에러가 발생할 확률이 높아지게 되는 것이다.
다시 정리하면 두 신호 가우스 확률분포의 겹치는 면적을 줄이기 위해서는 분산이 작아야 하고 분산이 작아지기 위해서는 진폭이 작아야 한다.
자 그러면 E와 -E가 정확히 겹쳐지는 중간지점을 detection point라 불렇는데 우리는 이 값을 알 필요가 있다. 즉 어떤 기준으로 오차가 발생했는지 수학적으로 판단할 필요가 있다는 뜻이다.
2. Detection Point
Detection Point를 계산하기 위해서는 베이지 이론과 결합확률에 대한 이해가 필요하다. 이를 깊게 설명하게 되면 상당히 복잡한 수학식을 유도해야 하므로 간단히 알아보고 넘어가겠다.
(1) 베이지 이론
베이지 이론은 사후확률과 사전확률 간의 관계를 정이한 것으로써 그 의미를 파악하면 베이즈 정리가 말하는 것을 알 수 있다. 우선 간단히 말하면 새로운 정보를 토대로 어떤 사건이 발생했다는 주장에 대한 신뢰도이다.
간단히 설명하면, S1신호를 보내서(사전확률) S2라 파악(사후확률) 또는 S2신호를 보내서 S1이라 파악하는 확률이라 생각하시면 편하겠다. 더 자세히 많은 예제를 알고 싶으면 구글에서 찾아보면 되겠다.
(2) Detection Point 정리

위의 수식을 보면 신호 S1과 S2를 송신할 때, S1이 S2로 또는 S2가 S1으로 판단될 확률을 베이지 이론으로 정리한 것이다. P(Z|S1) P(S1)이 P(Z|S2) P(S2) 보다 작으면 S2로 크면 S1으로 판단되는 것을 베이지 이론을 사용한 것이다. 정리하면 아래처럼 분수로 나타낼 수 있다.
그리고 S1과 S2의 평균되는 지점을 a1고 a2라고 가정하고 가우시안 확률분포를 이용해 정리하면 아래 수식과 같다. 일반 수식으로써 정리하게 되면 최종 detection point는 (a1 + a2) / 2로 나타낼 수 있다.

위 값들을 정리해 보면, 두신호를 송신 시 에러가 날 확률을 두 시호의 가우스 확률분포가 겹치는 넓이와 같다 이다. 이 넓이를 줄이기 위해서는 진폭의 크기를 작게 하는 것이다. 그리고 두 신호가 겹치는 중간지점을 detection point라 칭하였는데 이는 베이지 이론을 토대로 정리하면 (a1 + a2) / 2와 같다. 그러면 통신 신호 중 반극신호, 직교신호, 개폐신호에서 오차함수를 어떻게 나타내는 확인 해 보자
3. Q Function : 각 신호 전송 시 수신 측에서 에러가 발생할 확률. 오차함수와 동일하다.
우선 S1을 보내서 H2라 decision 하고 S2를 보내서 H1이라 decision 할 확률이 바로 에러가 날 확률과 동일하다. S1을 보내면 H1이라 decision 하는 것이 정상이기 때문이다. 이를 베이지 이론을 통해 정리하면 아래와 같다.

위 수식에서 중요한 것은 (a1 + a2) / 2가 클수록 가우스 분포의 오른쪽으로 가기 때문에 (면적이 작아지기 때문에) 성능이 좋게 된다.

위와 같이 유도하게 되면 최종적으로 Q함수가 유도되며 각 신호를 송신 시 수신 측에서 발생하게 되는 에러이다. 앞으로 Q함수를 이용하여 에러를 표현할 것이다.
(1) 반극신호의 Q함수
두 신호의 a1과 a2는 -루트 E,+루트 E로 표현되고 a1-a2는 아래 수식과 같이 표현된다.

(2) 직교신호의 Q함수
직교신호의 거리는 삼각함수 1:1 루트 2 공식에 의해서 아래와 같이 Q함수를 나타낼 수 있다. 반극신호보다 2배 작아진 것을 확이할 수 있고 전력에서 2배는 3dB 줄어든 것과 같다.

(3) 개폐신호의 Q함수
a1-a2는 루트 E 이므로 Q함수는 아래와 같고 직교신호보다 2배 작으므로 직교신호보다 3dB 줄어든 것과 같다.
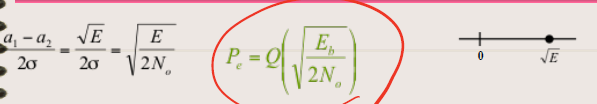
4. 정리
통신 신호에 따른 오차 함수를 알아보았으며, 이를 Q 함수로 표현하였다. 이를 위해 가우시안 확률 분포, 가우시안 적분, 베이지 이론, Detection point 유도와 의미, Q 함수, 각 신호의 Q 함수 등을 알아보았다.



