이전 포스팅에서 시계열 신호에 대한 변화 지점 탐지를 실시해 보았습니다. 이때, 우리는 변화 지점을 알고 있다고 가정하고 시뮬레이션을 해 보았는데 변화 지점을 모를 경우 어떻게 문제를 해결하는지 알아보겠습니다.
1. 변화 지점 탐지 시 변화지점 개수를 모를 경우
아래 그림을 확인해 보면 변화지점 2개일 때는 정확히 신호의 상승과 하강을 찾아낼 수 있으나 그렇지 않을 경우에는 과소탐지 또는 과적탐지를 하는 것을 알 수 있습니다. 그렇기 때문에 우리는 최적의 변화지점 개수를 우선적으로 알아내야 합니다.
(1) 변화지점 1개 : 과소탐지
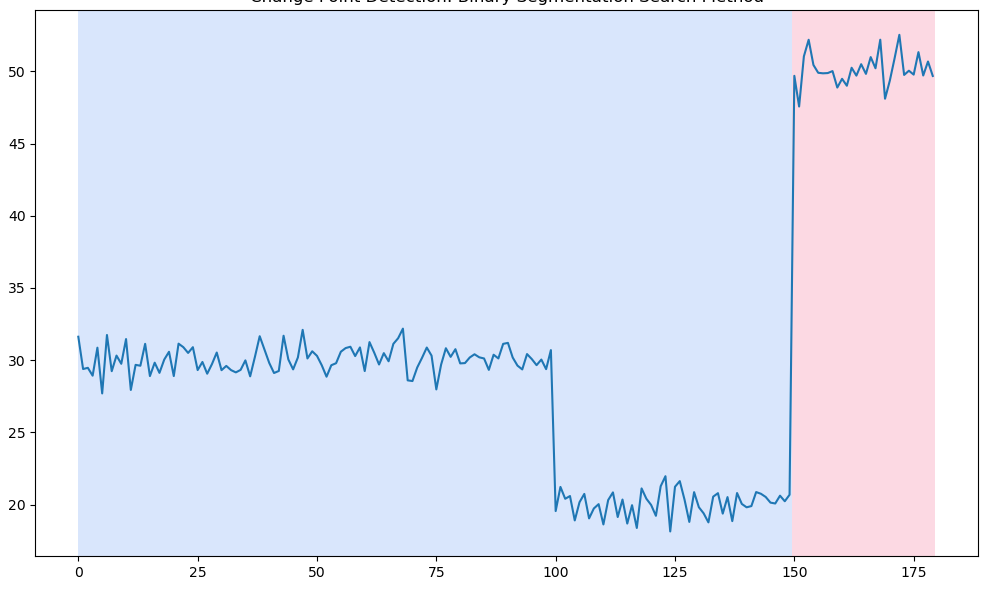
(2) 변화지점 2개
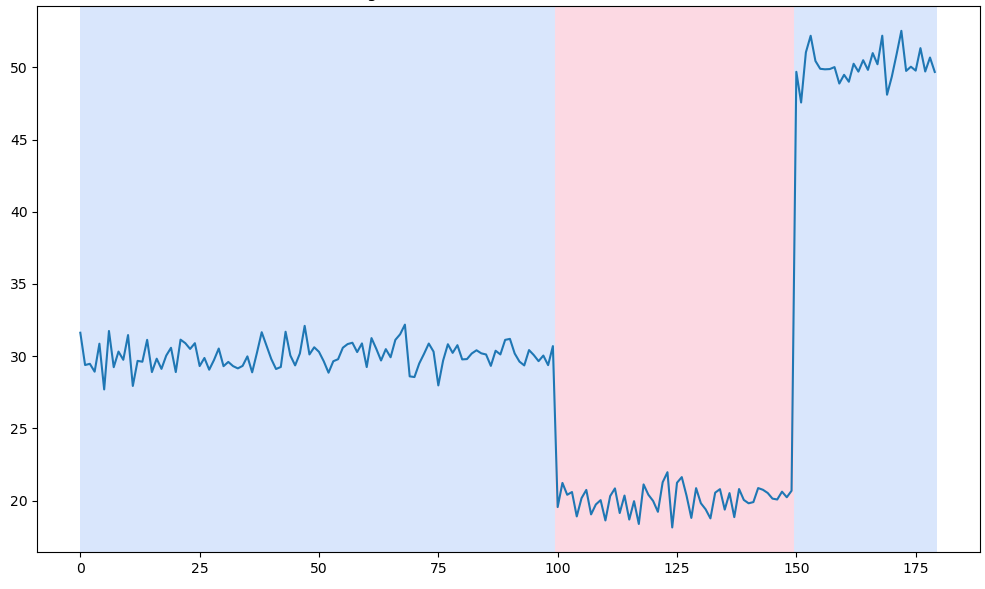
(3) 변화지점 4개 : 과적탐지
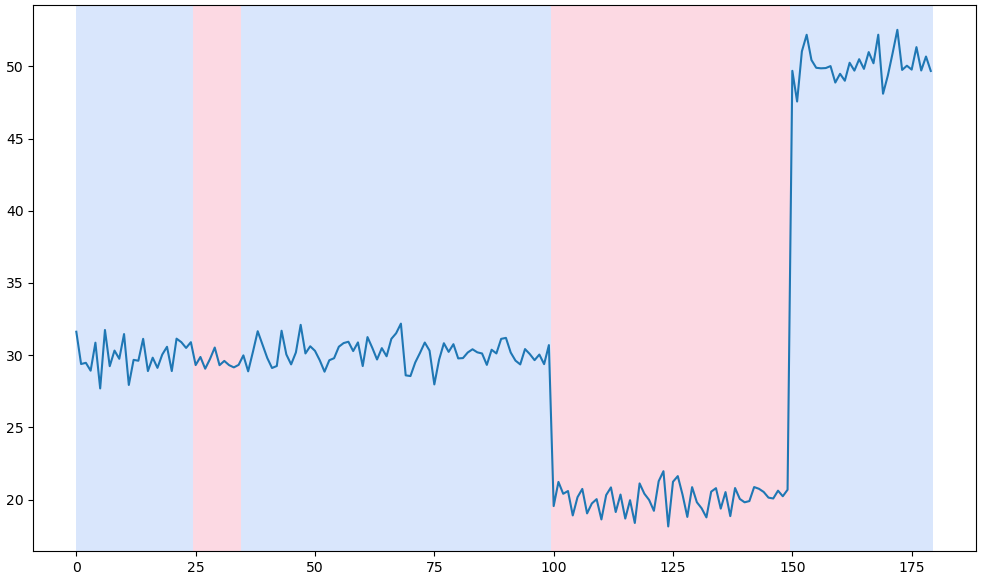
2. Elbow method : 변화 지점 탐지 시 최적의 군집 수 구하기
우선 군집(클러스터)의 개념부터 알아보도록 하겠습니다.
(1) 군집분석(클러스터링, clustering)
군집분석이란 개체들을 분류(classification) 하기 위한 기준이 없는 상태에서 주어진 데이터의 속성값들을 고려해 유사한 개체끼리 그룹(클러스터)화하는 방법입니다. 그룹 내 차이를 줄이고 그룹 간 차이는 최대화하도록 하여 대표성을 원리로 구현되는 것이 일반적입니다. 그중 비계층적 군집분석(Non-Hierachical Clustering)은, 급룹화할 유사도 측정 방식에 따라 최적의 그룹(cluster)을 계속 찾아나가는 방법으로 중심기반(Center-based) K-means 기법이 대표적입니다.
K-means 기법이란 유사한 데이터는 중심점(centroid)을 기반으로 분포할 것이다라는 가설로 시작하는 방법입니다. 구현 방법을 한번 알아보겠습니다. 우선 아래의 데이터를 어떻게 클러스터링 하는지 알아보시죠.

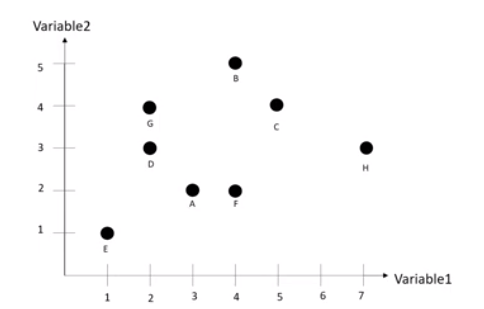
a. 초기점(k) 설정
- k는 중심점 (centroid)이자, 묶일 그룹(cluster)의 수와 같습니다. 위의 예로 보면 변화지점의 개수로 봐도 무방하죠.
- 우선 k를 2로 설정하고 A와 B를 임의의 중심점으로 가정합니다.
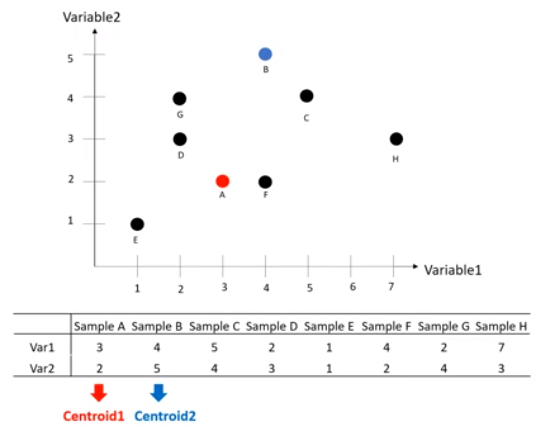
b. 그룹(cluster) 부여
- k개의 중심점과 개별데이터 간의 거리를 측정합니다.
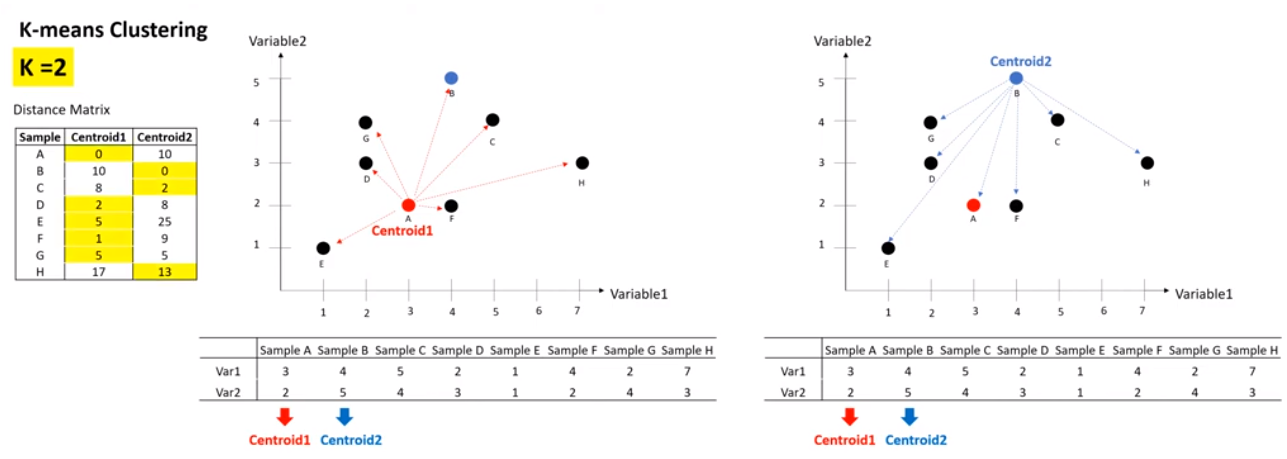
- 가장 가까운 중심점으로 데이터를 부여합니다. 위 데이터를 보면 centroid1은 A, D, E, F, G가 가깝고 centroid2는 B, C, H가 가깝습니다. 이렇게 클러스터링을 하면 됩니다.
c. 중심점(centroid) 업데이트
- 위의 클러스터링이 최선일까요? 아닙니다. 그래서 중심점을 계속 변경해 가며 업데이트해야 하는데 그 중심점은 클러스터의 평균값입니다.
- 할당된 데이터들의 평균값(mean)으로 새로운 중심점(centroid)을 업데이트합니다.
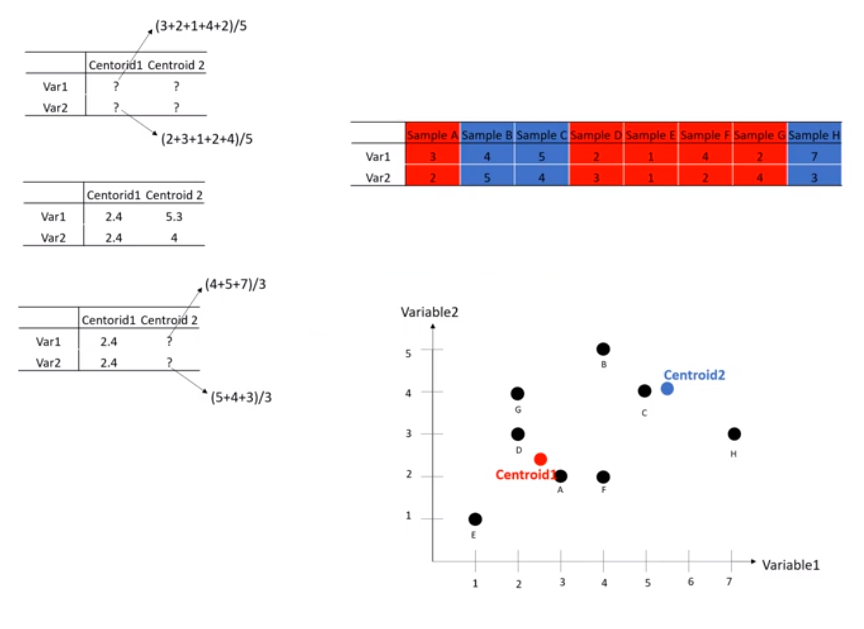
d. 최적화
- 위 작업을 n번 반복합니다.
- 변화가 수렴하면 작업을 중단합니다.

(2) Elbow method
위에서 군집화에 대하여 알아보았으며, 이제 Elbow method에 대하여 알아보시죠. Elbow mthod의 개념은 Cluster 간의 거리의 합을 나타내는 inertia가 급격히 떨어지는 구간이 생기는데 이 지점의 K 값을 군집을 개수로 사용하는 것입니다. 즉, 이 방법을 사용하면, 군집의 개수를 알 수 있다는 뜻이겠지요.
아래 그림을 확인해 보시면 군집의 개수가 2일 때부터 유클리드 거리가 확 떨어지는 것을 확인할 수 있습니다. 즉, K=2를 선택하면 되겠지요. 이때 그래프의 생김새가 팔꿈치 모양을 닮았다고 하여 Elbow mthod라 부릅니다.
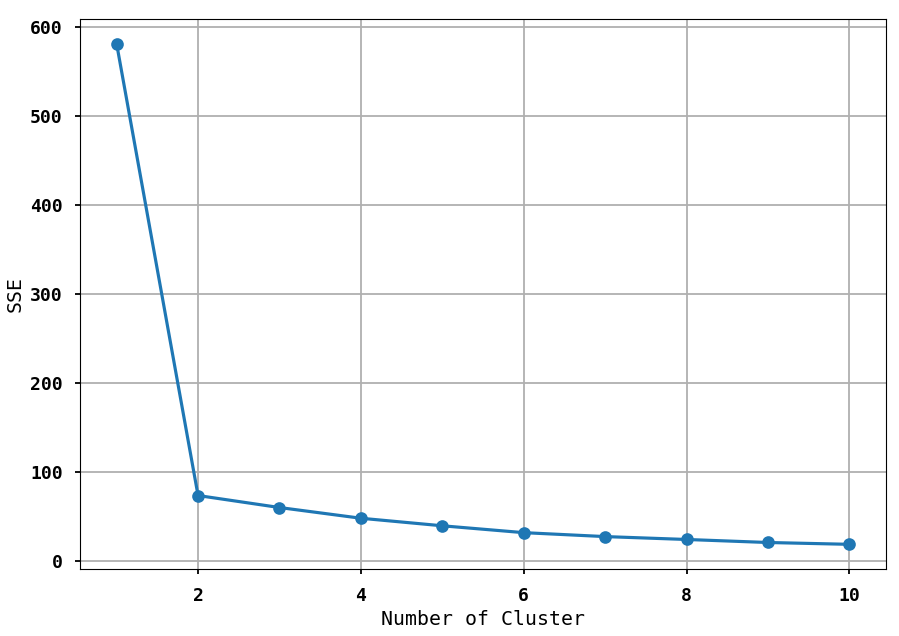
3. 정리
자 그러면 정리해 봅시다.
(1) 우리는 특정 데이터를 그룹화시켜야 합니다. 그 말인 즉 데이터의 변화지점들의 모임이라고 봐도 무방합니다.
(2) 그룹화를 위해서는 몇 개의 그룹이 있는지 초기 설정을 해 줘야 합니다. 그래야 각 그룹의 중심점을 바탕으로 상호 거리를 계산하여 그룹화를 할 수 있기 때문입니다.
(3) 몇개의 그룹이 있는지 알기 위해서 Elbow method를 사용합니다. 각 그룹마다의 거리의 합을 계산합니다. 그 거리의 합이 최소화될 때 그 지점이 바로 그룹의 최종 개수입니다.
(4) 그룹의 최종 개수도 계산되었으니, 최종 개수에 따라 각 그룹 간 거리를 계산하여 최적의 클러스터링을 해줍니다.
(5) 클러스터링이 되면, 그에 따른 변화 지점 탐지기법을 사용하면 되겠지요. 그러면 데이터의 변화지점을 최종적으로 계산할 수 있게 됩니다.
여기까지 하시면, 데이터가 어디서 변하는 지 알 수 있게 됩니다. 이러한 기법들이 머신러닝에서도 많이들 사용된다고 하는군요. 저는 저에게 맞는 코딩을 한번 해봐야겠습니다. 수고하셨습니다.
'대학 과목 > 빔 포밍(Beam Forming)' 카테고리의 다른 글
| Change Point Analysis : 데이터의 평균, 분산 변화 지점을 찾는 분석 기술(PELT, Anomaly), 주식 응용 가능 (4) | 2023.05.14 |
|---|---|
| 연속 웨이블릿 변환(Continuous Wavelet Transform) 스케일과 주파수의 관계 그리고 예제 (20) | 2023.05.07 |
| 웨이블릿(Wavelet) 변환(Transform) 상세 설명(그림 참조) (28) | 2023.05.07 |
| 웨이블릿(Wavelet) 변환의 개념(수식 없음) (7) | 2023.05.05 |
| 빔포밍(Beam Forming)의 개념과 이를 위한 구면좌표계(Spherical Coordinate) (20) | 2023.03.27 |



