극한이란 임의의 변수가 특정값에 무한히 가까워질 때를 일컫는 말입니다. 머신러닝에서는 특정 입력 데이터 값이 a로 한없이 가까워질 때 출력이 무엇이 나올까 유추하는 것인데 아래 예제를 통해 한번 알아보겠습니다.
1. 극한의 개념
아래는 극한 수식인데 x의 값이 a에 무한이 가까워질 때 출력되는 y값은 L이란 뜻입니다. 조금 난해할 수 있으니 예제를 통해 한번 알아보겠습니다.

아래 예제에서 x축의 a값이 1로 무한이 가까워질때 출력 y값은 1이 나오게 됩니다. 그리고 x축의 a값이 2로 무한이 가까워질 때 출력 y값은 2가 나오게 되고요. 간단하죠? 이게 극한입니다.
이때, f(x)는 y와 동급이라고 생각하시면 되겠습니다. 머신러닝에서도 바둑 시합을 할 때 a라는 수를 두면 y라는 결과가 나온다라는 것을 계속학습하게 됩니다. y가 승리 또는 패배이겠지요.

2. 극한이 존재할 수 있는 조건
좌극한과 우 극한을 살펴보겠습니다. 좌 극한은 왼쪽에서 가까워지는 것이고 우 극한은 오른쪽에서 가까워지는 것입니다. 이 것이 왜 중요한지 아래 예제를 통해 알아보겠습니다.

위의 그림을 보시면 우극한은 +로 좌 극한은 -로 표현되어 있습니다. 그리고 아래 그림 예제를 보시면 sgn 함수로 부호를 결정해주는 특징이 있으며 x가 0으로 무한히 접근할 때, 우 극한 시(우측에서 접근 시) y값 출력은 +1이 되고 좌 극한 시(좌측에서 접근 시) y값 축력은 -1이 되는 것을 확인할 수 있습니다.

자 그럼 1차함수의 극한 예제와 sgn 함수의 극한 예제가 있는데 무엇이 극한값이 존재하는 함수일까요? 1차 함수 예제는 좌 극한과 우 극한값이 동일합니다. 하지만 sgn 함수 예제는 좌 극한과 우 극한값이 상이하죠? 그렇습니다. 극한값이 존재하려면 좌극한과 우 극한값이 같아야 하고 수식으로는 아래와 같습니다.
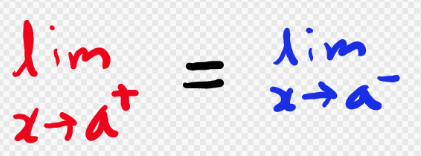
3. 극한의 연속성(Continuity)
극한의 연속성은 쉽게 말해 끊어지지 않고 연속되었다고 생각하시면 됩니다. 즉 극한이 존재해야 하고, x의 값이 a로 수렴할 때 출력 y의 값도 a와 연관성이 있어야 합니다.

그리고 극한의 연속성을 구간에서도 아래와 같이 표현할 수 있습니다. 우선 ∀기호는 "모든"이라는 뜻입니다. 모든 a는 x1과 x2의 범위에 들어간다는 뜻입니다. 즉, x1과 x 2구간에서 모든 a는 연속하다는 뜻이죠.

4. 극한과 점근선(Asymptotes)
점근선은 무한이 뻗는 곡선에서 어떠한 직선(x축 또는 y축)과의 거리가 0에 수렴해간다면 이 때의 직선을 점근선이라고 합니다.
점근선은 아래와 같이 나타낼 수 있습니다.
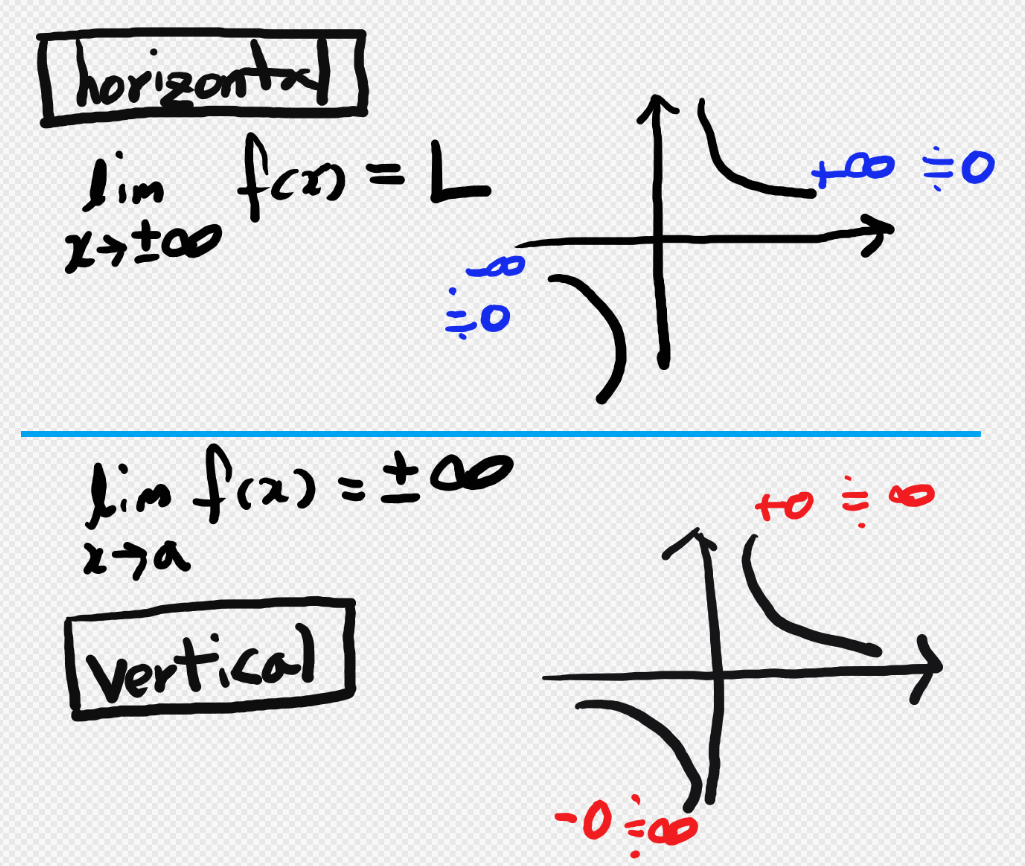
(1) Horizontal 점근선 : 아래와 같이 x축이 무한대로 가까워 질때 특정 L값에 수렴한다는 것입니다.
(2) Vertical 점근선 : y축이 0에 가까워 질 수록 무한대의 값을 가진다는 것입니다.
극한의 개념은 다양한 데이터를 수렴을 시키기 위한 것입니다. 다양한 고양이 얼굴(찌그러진, 길쭉한 등등)을 가지고 수렴시켜 고양이라는 값을 유추하거나, 다양한 주식 차트를 수렴시켜 롱 또는 숏 포지션을 예측하는 등의 행위를 할 수 있습니다. 너무 어렵게 생각하지 마시고 이런 것이 있구나라고 넘어가시면 될 것 같습니다.
'머신러닝(Machine Learning) > 기초수학' 카테고리의 다른 글
| 미분법의 다양한 공식들 : 상수, 멱함수, 지수 함수, 로그 함수, 삼각 함수, 기타 (6) | 2022.11.12 |
|---|---|
| 미적분학(머신러닝) : 평균 변화율과 순간 변화율, 미분 계수, 도함수 (8) | 2022.11.06 |
| 머신러닝/딥러닝을 위한 매개변수 모델링(Parametric Models) 기초 (12) | 2022.10.21 |
| 선형 함수(Linear Function) : 선형 결정 경계, 선형성, homogeneity, additivity (10) | 2022.09.25 |
| 함수의 대칭 이동과 변환(평행/수직) 그리고 정반사 및 우/기함수 (10) | 2022.09.25 |



