선형대수학 기초[1강]: 벡터의 덧셈, 뺄셈 및 스칼라배(파이썬 코드 포함)

1. 개요

 이 포스트에서는 선형대수학의 기초 개념인 **벡터(Vector)**의 기본 연산에 대해 알아본다.  벡터가 무엇인지 정의하고, 벡터의 크기와 방향 같은 특성을 설명한 뒤, 벡터 덧셈과 뺄셈, 그리고 **스칼라배(Scalar multiplication)**를 다루었다. 벡터의 덧셈과 뺄셈은 각 성분별로 이루어지며, 스칼라배는 벡터에 숫자를 곱하여 크기를 조절하는 연산이다. 이러한 기본 개념을 통해 2차원 평면상의 모든 벡터를 표현할 수 있다는 중요한 사실도 함께 소개된다.

 

  마지막에서는 파이썬 코드로 시각적인 결과도 확인할 수 있다.

2. 벡터와 크기·방향

 벡터는 여러 수를 한 줄로 나열하여 표현되는 양으로, 좌표평면에서는 화살표(방향과 크기를 가진 선)로 나타낼 수 있다.
예를 들어, 벡터 [3, 2]는 x축 방향으로 3, y축 방향으로 2만큼 향하는 화살표로 표현된다.
이 벡터의 크기는 피타고라스 정리에 따라 아래와 같이 계산된다.

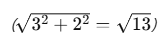
또한, 벡터의 방향은 양의 x축과 아래와 같은 각도를 이룬다.

 

 벡터는 위치와 무관하게 크기와 방향만 같으면 동일한 벡터로 간주된다. 즉, 시작점이 달라도 화살표의 끝점이 동일한 두 벡터는 같은 벡터이다.

 

3. 벡터의 덧셈

두 벡터의 합은 각 대응되는 성분끼리 더해서 구한다.
보다 공식적으로, n차원 벡터 u와 w는 아래와 같이 표현된다.

이때 두 벡터의 덧셈은 아래와 같다.

예를 들어, u=[2, 3]와 w = [1, -1]라면,
각 성분을 더하여

벡터 덧셈은 교환법칙과 결합법칙이 성립한다는 점도 중요하다. 아래 그림을 보시면 1, --1을 평행이동한 것이다.

4. 벡터의 뺄셈

벡터 뺄셈은 덧셈과 유사하게 각 성분끼리 빼서 새로운 벡터를 얻는 연산이다.
일반적으로 아래와 같이 표현한다.

 

예를 들어, u=[2, 3]와 w=[1, −1]의 경우에는

 여기서 −w는 벡터 w와 크기는 같지만 방향이 반대인 벡터이다.

뺄

5. 스칼라배

벡터의 스칼라배(scalar multiplication)는 벡터에 스칼라(일반적인 숫자)를 곱하는 연산이다.
벡터 u에 스칼라 c를 곱하면 아래와 같이 각 성분에 c가 곱해진다.

 

예를 들어, u=[2, 3]에 2를 곱하면

 

양의 스칼라는 벡터의 크기만 늘리거나 줄이고, 음의 스칼라는 방향을 반대로 뒤집는다.

6. 벡터 연산을 통한 공간 구성

벡터의 덧셈과 스칼라배를 조합하면 2차원 평면의 모든 벡터를 표현할 수 있다.
예를 들어, 2차원 단위벡터 [1,0]과 [0,1]에 임의의 실수 a, b를 곱해 더하면

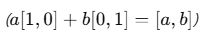
즉, a와 b에 다양한 값을 넣어 평면상의 모든 점 [a, b]를 만들어낼 수 있다.
이때 [1,0]과 [0,1]은 단위벡터라 하며, 크기가 1인 벡터이다.
이 개념은 선형대수의 기초로 매우 중요하다.

7. 파이썬 코드

import numpy as np
import matplotlib.pyplot as plt
import math

# 2x2 서브플롯 생성
fig, axs = plt.subplots(2, 2, figsize=(12, 12))
fig.suptitle("Vector Operations: Magnitude/Direction, Addition, Subtraction, Scalar Multiplication", fontsize=16)

# 1. 벡터의 크기와 방향: v = [3, 2]
ax = axs[0, 0]
v = np.array([3, 2])
ax.arrow(0, 0, v[0], v[1], head_width=0.2, head_length=0.3, fc='blue', ec='blue', length_includes_head=True)
ax.text(v[0] + 0.2, v[1] + 0.2, 'v = [3,2]', fontsize=12, color='blue')
# 벡터의 크기 (sqrt(3^2+2^2))와 방향 (atan2(2,3))
magnitude = math.sqrt(3**2 + 2**2)
theta = math.degrees(math.atan2(v[1], v[0]))
ax.text(v[0]/2, v[1]/2, f"M = {magnitude:.2f}", fontsize=12, color='black')
ax.text(v[0]/2, v[1]/2 - 0.5, f"{theta:.1f}°", fontsize=12, color='black')
ax.set_title("Vector: Magnitude & Direction")
ax.axhline(0, color='gray', lw=0.5)
ax.axvline(0, color='gray', lw=0.5)
ax.set_xlim(-1, 4)
ax.set_ylim(-1, 4)
ax.set_aspect('equal')

# 2. 벡터 덧셈: v = [3,2]와 w = [-2,1] -> v + w = [1,3]
ax = axs[0, 1]
v = np.array([2, 3])
w = np.array([1, -1])
v_plus_w = v + w
# v를 원점에서 시작
ax.arrow(0, 0, v[0], v[1], head_width=0.2, head_length=0.3, fc='blue', ec='blue', length_includes_head=True)
# w를 v의 끝에서 시작 (머리-꼬리 방식)
ax.arrow(v[0], v[1], w[0], w[1], head_width=0.2, head_length=0.3, fc='green', ec='green', length_includes_head=True)
# 덧셈 결과: v + w
ax.arrow(0, 0, v_plus_w[0], v_plus_w[1], head_width=0.2, head_length=0.3, fc='red', ec='red', length_includes_head=True)
ax.text(v[0] + 0.2, v[1] + 0.2, 'v', fontsize=12, color='blue')
ax.text(v[0] + w[0] + 0.2, v[1] + w[1] + 0.2, 'w', fontsize=12, color='green')
ax.text(v_plus_w[0] + 0.2, v_plus_w[1] + 0.2, 'v+w', fontsize=12, color='red')
ax.set_title("Vector Addition")
ax.axhline(0, color='gray', lw=0.5)
ax.axvline(0, color='gray', lw=0.5)
ax.set_xlim(-3, 4)
ax.set_ylim(-1, 4)
ax.set_aspect('equal')

# 3. 벡터 뺄셈: v = [3,2]와 w = [-2,1] -> v - w = [5,1]
ax = axs[1, 0]
v = np.array([2, 3])
w = np.array([1, -1])
v_minus_w = v - w
# v는 원점에서 시작
ax.arrow(0, 0, v[0], v[1], head_width=0.2, head_length=0.3, fc='blue', ec='blue', length_includes_head=True)
# -w를 원점에서 표시 (w의 반대 방향)
ax.arrow(0, 0, -w[0], -w[1], head_width=0.2, head_length=0.3, fc='green', ec='green', length_includes_head=True)
# v - w를 원점에서 표시
ax.arrow(0, 0, v_minus_w[0], v_minus_w[1], head_width=0.2, head_length=0.3, fc='red', ec='red', length_includes_head=True)
ax.text(v[0] + 0.2, v[1] + 0.2, 'v', fontsize=12, color='blue')
ax.text(-w[0] + 0.2, -w[1] + 0.2, '-w', fontsize=12, color='green')
ax.text(v_minus_w[0] + 0.2, v_minus_w[1] + 0.2, 'v - w', fontsize=12, color='red')
ax.set_title("Vector Subtraction")
ax.axhline(0, color='gray', lw=0.5)
ax.axvline(0, color='gray', lw=0.5)
ax.set_xlim(-1, 6)
ax.set_ylim(-1, 4)
ax.set_aspect('equal')

# 4. 벡터 스칼라배: u = [2,1] -> 2*u = [4,2]와 -2*u = [-4,-2]
ax = axs[1, 1]
u = np.array([2, 3])
u2 = 2 * u
u_neg2 = -2 * u
# 원래 벡터 u
ax.arrow(0, 0, u[0], u[1], head_width=0.2, head_length=0.3, fc='blue', ec='blue', length_includes_head=True)
# 2배 스칼라배: 2*u
ax.arrow(0, 0, u2[0], u2[1], head_width=0.2, head_length=0.3, fc='red', ec='red', length_includes_head=True)
# -2배 스칼라배: -2*u
ax.arrow(0, 0, u_neg2[0], u_neg2[1], head_width=0.2, head_length=0.3, fc='green', ec='green', length_includes_head=True)
ax.text(u[0] + 0.2, u[1] + 0.2, 'u', fontsize=12, color='blue')
ax.text(u2[0] + 0.2, u2[1] + 0.2, '2u', fontsize=12, color='red')
ax.text(u_neg2[0] + 0.2, u_neg2[1] + 0.2, '-2u', fontsize=12, color='green')
ax.set_title("Scalar Multiplication")
ax.axhline(0, color='gray', lw=0.5)
ax.axvline(0, color='gray', lw=0.5)
ax.set_xlim(-5, 5)
ax.set_ylim(-5, 5)
ax.set_aspect('equal')

# 최종 플롯 파일로 저장 (.plt 확장자 사용)
plt.savefig("vector_operations.plt")
plt.show()